Papers

2024

1. arXiv

   Sequential Knockoffs for Variable Selection in Reinforcement Learning

   Tao Ma*, Jin Zhu*, Hengrui Cai, Zhengling Qi, Yunxiao Chen, and 2 more authors

   arXiv preprint arXiv:2303.14281, 2024

   Abs PDF

   In real-world applications of reinforcement learning, it is often challenging to obtain a state representation that is parsimonious and satisfies the Markov property without prior knowledge. Consequently, it is common practice to construct a state larger than necessary, e.g., by concatenating measurements over contiguous time points. However, needlessly increasing the dimension of the state may slow learning and obfuscate the learned policy. We introduce the notion of a minimal sufficient state in a Markov decision process (MDP) as the subvector of the original state under which the process remains an MDP and shares the same reward function as the original process. We propose a novel SEquEntial Knockoffs (SEEK) algorithm that estimates the minimal sufficient state in a system with high-dimensional complex nonlinear dynamics. In large samples, the proposed method achieves selection consistency. As the method is agnostic to the reinforcement learning algorithm being applied, it benefits downstream tasks such as policy learning. Empirical experiments verify theoretical results and show the proposed approach outperforms several competing methods regarding variable selection accuracy and regret.

2. JMLR

   skscope: Fast Sparsity-Constrained Optimization in Python

   Zezhi Wang, Junxian Zhu, Xueqin Wang, Jin Zhu, Peng Chen, and 3 more authors

   Journal of Machine Learning Research, 2024

   Abs PDF Code

   Applying iterative solvers on sparsity-constrained optimization (SCO) requires tedious mathematical deduction and careful programming/debugging that hinders these solvers’ broad impact. In the paper, the library skscope is introduced to overcome such an obstacle. With skscope, users can solve the SCO by just programming the objective function. The convenience of skscope is demonstrated through two examples in the paper, where sparse linear regression and trend filtering are addressed with just four lines of code. More importantly, skscope’s efficient implementation allows state-of-the-art solvers to quickly attain the sparse solution regardless of the high dimensionality of parameter space. Numerical experiments reveal the available solvers in skscope can achieve up to 80x speedup on the competing relaxation solutions obtained via the benchmarked convex solver. skscope is published on the Python Package Index (PyPI) and Conda, and its source code is available at: https://github.com/abess-team/skscope.

3. AISTATS

   Robust Offline Reinforcement Learning with Heavy-Tailed Rewards

   Jin Zhu, Runzhe Wan, Zhengling Qi, Shikai Luo, and Chengchun Shi

   In The 27th International Conference on Artificial Intelligence and Statistics, 2024

   Abs PDF Code

   This paper endeavors to augment the robustness of offline reinforcement learning (RL) in scenarios laden with heavy-tailed rewards, a prevalent circumstance in real-world applications. We propose two algorithmic frameworks, ROAM and ROOM, for robust off-policy evaluation (OPE) and offline policy optimization (OPO), respectively. Central to our frameworks is the strategic incorporation of the median-of-means method with offline RL, enabling straightforward uncertainty estimation for the value function estimator. This not only adheres to the principle of pessimism in OPO but also adeptly manages heavy-tailed rewards. Theoretical results and extensive experiments demonstrate that our two frameworks outperform existing methods on the logged dataset exhibits heavy-tailed reward distributions.

2023

1. JASA

   Nonparametric Statistical Inference via Metric Distribution Function in Metric Spaces

   Xueqin Wang*, Jin Zhu*, Wenliang Pan*, Junhao Zhu*, and Heping Zhang*

   Journal of the American Statistical Association, 2023

   Abs PDF Code

   Distribution function is essential in statistical inference, and connected with samples to form a directed closed loop by the correspondence theorem in measure theory and the Glivenko-Cantelli and Donsker properties. This connection creates a paradigm for statistical inference. However, existing distribution functions are defined in Euclidean spaces and no longer convenient to use in rapidly evolving data objects of complex nature. It is imperative to develop the concept of distribution function in a more general space to meet emerging needs. Note that the linearity allows us to use hypercubes to define the distribution function in a Euclidean space, but without the linearity in a metric space, we must work with the metric to investigate the probability measure. We introduce a class of metric distribution functions through the metric between random objects and a fixed location in metric spaces. We overcome this challenging step by proving the correspondence theorem and the Glivenko-Cantelli theorem for metric distribution functions in metric spaces that lie the foundation for conducting rational statistical inference for metric space-valued data. Then, we develop homogeneity test and mutual independence test for non-Euclidean random objects, and present comprehensive empirical evidence to support the performance of our proposed methods.

2. arXiv

   A SIMPLE Approach to Provably Reconstruct Ising Model with Global Optimality

   Junxian Zhu*, Xuanyu Chen*, Jin Zhu*, Xueqin Wang, and Heping Zhang

   arXiv, 2023

   Abs PDF

   Reconstruction of interaction network between random events is a critical problem arising from statistical physics and politics to sociology, biology, and psychology, and beyond. The Ising model lays the foundation for this reconstruction process, but finding the underlying Ising model from the least amount of observed samples in a computationally efficient manner has been historically challenging for half a century. By using the idea of sparsity learning, we present a approach named SIMPLE that has a dominant sample complexity from theoretical limit. Furthermore, a tuning-free algorithm is developed to give a statistically consistent solution of SIMPLE in polynomial time with high probability. On extensive benchmarked cases, the SIMPLE approach provably reconstructs underlying Ising models with global optimality. The application on the U.S. senators voting in the last six congresses reveals that both the Republicans and Democrats noticeably assemble in each congresses; interestingly, the assembling of Democrats is particularly pronounced in the latest congress.

3. arXiv

   A Consistent and Scalable Algorithm for Best Subset Selection in Single Index Models

   Borui Tang*, Jin Zhu*, Junxian Zhu*, Xueqin Wang, and Heping Zhang

   arXiv, 2023

   Abs PDF

   Analysis of high-dimensional data has led to increased interest in both single index models (SIMs) and best subset selection. SIMs provide an interpretable and flexible modeling framework for high-dimensional data, while best subset selection aims to find a sparse model from a large set of predictors. However, best subset selection in high-dimensional models is known to be computationally intractable. Existing methods tend to relax the selection, but do not yield the best subset solution. In this paper, we directly tackle the intractability by proposing the first provably scalable algorithm for best subset selection in high-dimensional SIMs. Our algorithmic solution enjoys the subset selection consistency and has the oracle property with a high probability. The algorithm comprises a generalized information criterion to determine the support size of the regression coefficients, eliminating the model selection tuning. Moreover, our method does not assume an error distribution or a specific link function and hence is flexible to apply. Extensive simulation results demonstrate that our method is not only computationally efficient but also able to exactly recover the best subset in various settings (e.g., linear regression, Poisson regression, heteroscedastic models).

4. arXiv

   Best-subset selection in generalized linear models: A fast and consistent algorithm via splicing technique

   Junxian Zhu, Jin Zhu, Borui Tang, Xuanyu Chen, Hongmei Lin, and 1 more author

   arXiv, 2023

   Abs PDF

   In high-dimensional generalized linear models, it is crucial to identify a sparse model that adequately accounts for response variation. Although the best subset section has been widely regarded as the Holy Grail of problems of this type, achieving either computational efficiency or statistical guarantees is challenging. In this article, we intend to surmount this obstacle by utilizing a fast algorithm to select the best subset with high certainty. We proposed and illustrated an algorithm for best subset recovery in regularity conditions. Under mild conditions, the computational complexity of our algorithm scales polynomially with sample size and dimension. In addition to demonstrating the statistical properties of our method, extensive numerical experiments reveal that it outperforms existing methods for variable selection and coefficient estimation. The runtime analysis shows that our implementation achieves approximately a fourfold speedup compared to popular variable selection toolkits like glmnet and ncvreg.

5. ICML

   An Instrumental Variable Approach to Confounded Off-Policy Evaluation

   Yang Xu, Jin Zhu, Chengchun Shi, Shikai Luo, and Rui Song

   In Proceedings of the 40th International Conference on Machine Learning, 2023

   Abs PDF

   Off-policy evaluation (OPE) aims to estimate the return of a target policy using some pre-collected observational data generated by a potentially different behavior policy. In many cases, there exist unmeasured variables that confound the action-reward or action-next-state relationships, rendering many existing OPE approaches ineffective. This paper develops an instrumental variable (IV)-based method for consistent OPE in confounded sequential decision making. Similar to single-stage decision making, we show that IV enables us to correctly identify the target policy’s value in infinite horizon settings as well. Furthermore, we propose a number of policy value estimators and illustrate their effectiveness through extensive simulations and real data analysis from a world-leading short-video platform.

6. IJOC

   A Splicing Approach to Best Subset of Groups Selection

   Yanhang Zhang*, Junxian Zhu*, Jin Zhu*, and Xueqin Wang

   INFORMS Journal on Computing, 2023

   Abs PDF Code

   Best subset of groups selection (BSGS) is the process of selecting a small part of nonoverlapping groups to achieve the best interpretability on the response variable. It has attracted increasing attention and has far-reaching applications in practice. However, due to the computational intractability of BSGS in high-dimensional settings, developing efficient algorithms for solving BSGS remains a research hotspot. In this paper, we propose a group-splicing algorithm that iteratively detects the relevant groups and excludes the irrelevant ones. Moreover, coupled with a novel group information criterion, we develop an adaptive algorithm to determine the optimal model size. Under certain conditions, it is certifiable that our algorithm can identify the optimal subset of groups in polynomial time with high probability. Finally, we demonstrate the efficiency and accuracy of our methods by comparing them with several state-of-the-art algorithms on both synthetic and real-world data sets.

2022

1. arXiv

   Quantiles, Ranks and Signs in Metric Spaces

   Hang Liu, Xueqin Wang, and Jin Zhu

   arXiv, 2022

   Abs PDF

   Non-Euclidean data is currently prevalent in many fields, necessitating the development of novel concepts such as distribution functions, quantiles, rankings, and signs for these data in order to conduct nonparametric statistical inference. This study provides new thoughts on quantiles, both locally and globally, in metric spaces. This is realized by expanding upon metric distribution function proposed by Wang et al. (2021). Rank and sign are defined at both the local and global levels as a natural consequence of the center-outward ordering of metric spaces brought about by the local and global quantiles. The theoretical properties are established, such as the root-n consistency and uniform consistency of the local and global empirical quantiles and the distribution-freeness of ranks and signs. The empirical metric median, which is defined here as the 0th empirical global metric quantile, is proven to be resistant to contaminations by means of both theoretical and numerical approaches. Quantiles have been shown valuable through extensive simulations in a number of metric spaces. Moreover, we introduce a family of fast rank-based independence tests for a generic metric space. Monte Carlo experiments show good finite-sample performance of the test. Quantiles are demonstrated in a real-world setting by analysing hippocampal data.

2. JMLR

   abess: A Fast Best-Subset Selection Library in Python and R

   Jin Zhu, Xueqin Wang, Liyuan Hu, Junhao Huang, Kangkang Jiang, and 3 more authors

   Journal of Machine Learning Research, 2022

   Abs PDF Code Poster

   We introduce a new library named abess that implements a unified framework of best-subset selection for solving diverse machine learning problems, e.g., linear regression, classification, and principal component analysis. Particularly, abess certifiably gets the optimal solution within polynomial time with high probability under the linear model. Our efficient implementation allows abess to attain the solution of best-subset selection problems as fast as or even 20x faster than existing competing variable (model) selection toolboxes. Furthermore, it supports common variants like best subset of groups selection and l2 regularized best-subset selection. The core of the library is programmed in C++. For ease of use, a Python library is designed for convenient integration with scikit-learn, and it can be installed from the Python Package Index (PyPI). In addition, a user-friendly R library is available at the Comprehensive R Archive Network (CRAN). The source code is available at: https://github.com/abess-team/abess.

3. JASA

   Off-Policy Confidence Interval Estimation with Confounded Markov Decision Process

   Chengchun Shi, Jin Zhu, Shen Ye, Shikai Luo, Hongtu Zhu, and 1 more author

   Journal of the American Statistical Association, 2022

   Abs PDF Code

   This paper is concerned with constructing a confidence interval for a target policy’s value offline based on a pre-collected observational data in infinite horizon settings. Most of the existing works assume no unmeasured variables exist that confound the observed actions. This assumption, however, is likely to be violated in real applications such as healthcare and technological industries. In this paper, we show that with some auxiliary variables that mediate the effect of actions on the system dynamics, the target policy’s value is identifiable in a confounded Markov decision process. Based on this result, we develop an efficient off-policy value estimator that is robust to potential model misspecification and provide rigorous uncertainty quantification. Our method is justified by theoretical results, simulated and real datasets obtained from ridesharing companies. A Python implementation of the proposed procedure is available at https://github.com/Mamba413/cope.

4. Paired-sample tests for homogeneity with/without confounding variables

   Minqiong Chen, Ting Tian, Jin Zhu, Wenliang Pan, and Xueqin Wang

   Statistics and Its Interface, 2022

   Abs

   In this article, we are concerned about testing the homogeneity on paired samples with or without confounding variables. These problems usually arise in clinical trials, psychological or sociological studies. We introduce new nonparametric tests for equality of two distributions or two conditional distributions of random vectors on paired samples. We show that their test statistics are consistent but have different asymptotic distributions under the null hypothesis, depending on whether confounding variables exist. The limit distribution of the test statistic is a mixed χ^2 distribution when testing the equality of two paired distributions, while it is a normal distribution when testing the equality of two conditional distributions of paired samples. We conduct several simulation studies to evaluate the finite-sample performance of our tests. Finally, we apply our tests on real data to illustrate their usefulness in the applications.

5. 

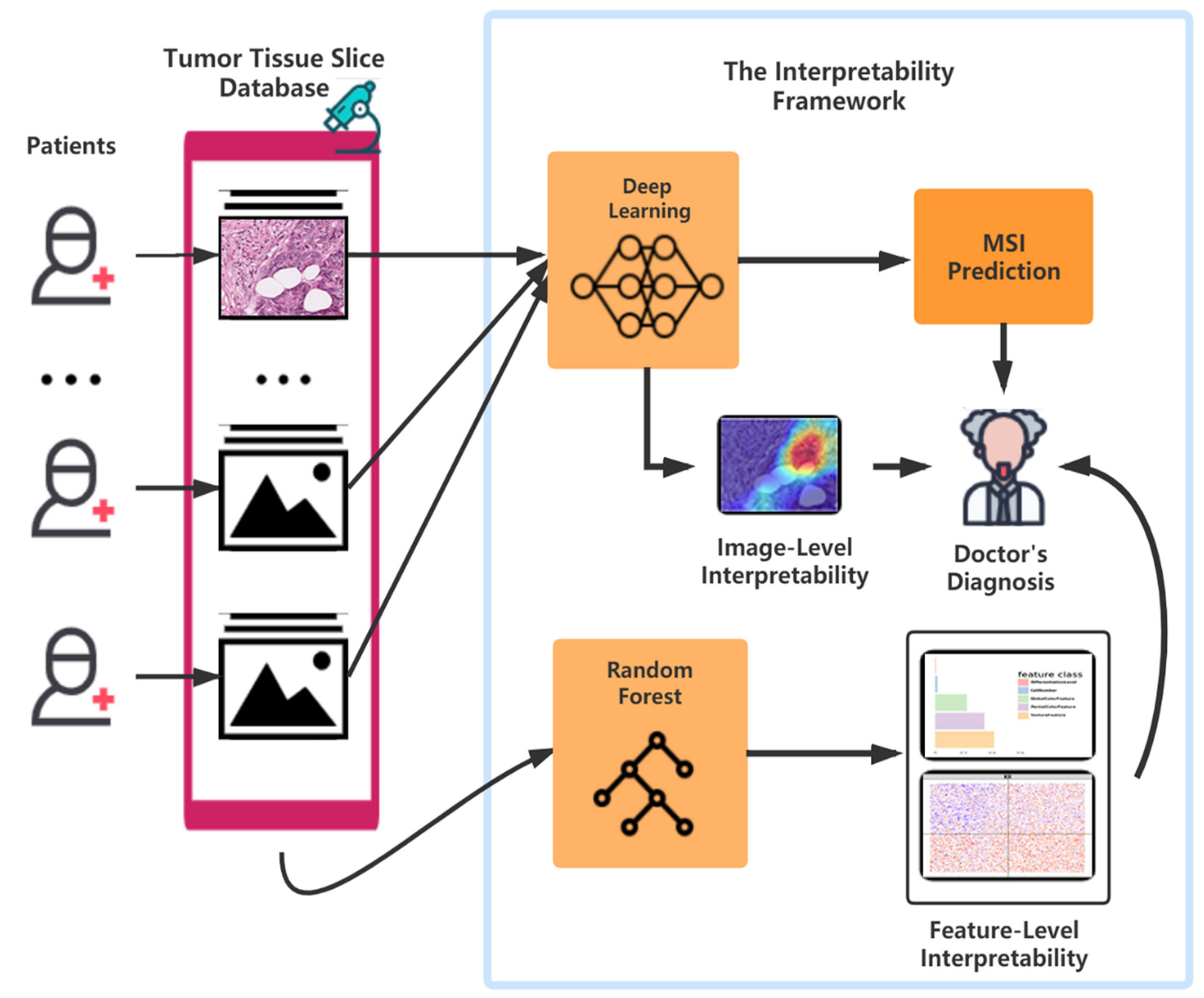   Computational Analysis of Pathological Image Enables Interpretable Prediction for Microsatellite Instability

   Jin Zhu, Wangwei Wu, Yuting Zhang, Shiyun Lin, Yukang Jiang, and 3 more authors

   Frontiers in Oncology, 2022

   PDF

2021

1. JSS

   Ball: An R package for detecting distribution difference and association in metric spaces

   Jin Zhu, Wenliang Pan, Wei Zheng, and Xueqin Wang

   Journal of Statistical Software, 2021

   Abs PDF Code

   The rapid development of modern technology has created many complex datasets in non-linear spaces, while most of the statistical hypothesis tests are only available in Euclidean or Hilbert spaces. To properly analyze the data with more complicated structures, efforts have been made to solve the fundamental test problems in more general spaces (Lyons 2013; Pan, Tian, Wang, and Zhang 2018; Pan, Wang, Zhang, Zhu, and Zhu 2020). In this paper, we introduce a publicly available R package Ball for the comparison of multiple distributions and the test of mutual independence in metric spaces, which extends the test procedures for the equality of two distributions (Pan et al. 2018) and the independence of two random objects (Pan et al. 2020). The Ball package is computationally efficient since several novel algorithms as well as engineering techniques are employed in speeding up the ball test procedures. Two real data analyses and diverse numerical studies have been performed, and the results certify that the Ball package can detect various distribution differences and complicated dependencies in complex datasets, e.g., directional data and symmetric positive definite matrix data.

2. 

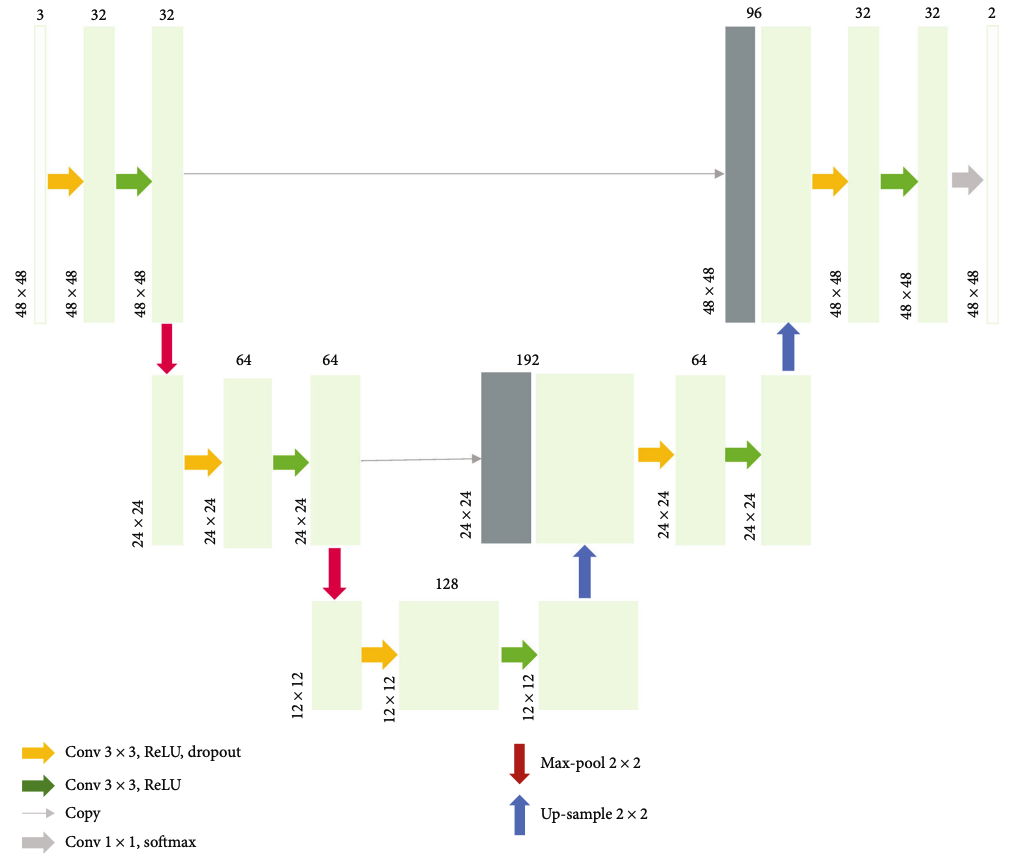   Segmentation of Laser Marks of Diabetic Retinopathy in the Fundus Photographs Using Lightweight U-Net

   Yukang Jiang, Jianying Pan, Ming Yuan, Yanhe Shen, Jin Zhu, and 8 more authors

   Journal of Diabetes Research, Oct 2021

   Abs

   Diabetic retinopathy (DR) is a prevalent vision-threatening disease worldwide. Laser marks are the scars left after panretinal photocoagulation, a treatment to prevent patients with severe DR from losing vision. In this study, we develop a deep learning algorithm based on the lightweight U-Net to segment laser marks from the color fundus photos, which could help indicate a stage or providing valuable auxiliary information for the care of DR patients. We prepared our training and testing data, manually annotated by trained and experienced graders from Image Reading Center, Zhongshan Ophthalmic Center, publicly available to fill the vacancy of public image datasets dedicated to the segmentation of laser marks. The lightweight U-Net, along with two postprocessing procedures, achieved an AUC of 0.9824, an optimal sensitivity of 94.16%, and an optimal specificity of 92.82% on the segmentation of laser marks in fundus photographs. With accurate segmentation and high numeric metrics, the lightweight U-Net method showed its reliable performance in automatically segmenting laser marks in fundus photographs, which could help the AI assist the diagnosis of DR in the severe stage.

2020

1. PNAS

   A polynomial algorithm for best subset selection problem

   JunXian Zhu, CanHong Wen, Jin Zhu, XueQin Wang, and HePing Zhang

   Proceedings of the National Academy of Sciences, Oct 2020

   Abs PDF Code

   Best-subset selection aims to find a small subset of predictors, so that the resulting linear model is expected to have the most desirable prediction accuracy. It is not only important and imperative in regression analysis but also has far-reaching applications in every facet of research, including computer science and medicine. We introduce a polynomial algorithm, which, under mild conditions, solves the problem. This algorithm exploits the idea of sequencing and splicing to reach a stable solution in finite steps when the sparsity level of the model is fixed but unknown. We define an information criterion that helps the algorithm select the true sparsity level with a high probability. We show that when the algorithm produces a stable optimal solution, that solution is the oracle estimator of the true parameters with probability one. We also demonstrate the power of the algorithm in several numerical studies.

2. JASA

   Ball covariance: A generic measure of dependence in banach space

   Wenliang Pan*, Xueqin Wang*, Heping Zhang*, Hongtu Zhu*, and Jin Zhu*

   Journal of the American Statistical Association, Oct 2020

   Abs

   Technological advances in science and engineering have led to the routine collection of large and complex data objects, where the dependence structure among those objects is often of great interest. Those complex objects (e.g., different brain subcortical structures) often reside in some Banach spaces, and hence their relationship cannot be well characterized by most of the existing measures of dependence such as correlation coefficients developed in Hilbert spaces. To overcome the limitations of the existing measures, we propose Ball Covariance as a generic measure of dependence between two random objects in two possibly different Banach spaces. Our Ball Covariance possesses the following attractive properties: (i) It is nonparametric and model-free, which make the proposed measure robust to model mis-specification; (ii) It is nonnegative and equal to zero if and only if two random objects in two separable Banach spaces are independent; (iii) Empirical Ball Covariance is easy to compute and can be used as a test statistic of independence. We present both theoretical and numerical results to reveal the potential power of the Ball Covariance in detecting dependence. Also importantly, we analyze two real datasets to demonstrate the usefulness of Ball Covariance in the complex dependence detection.

2019

1. 

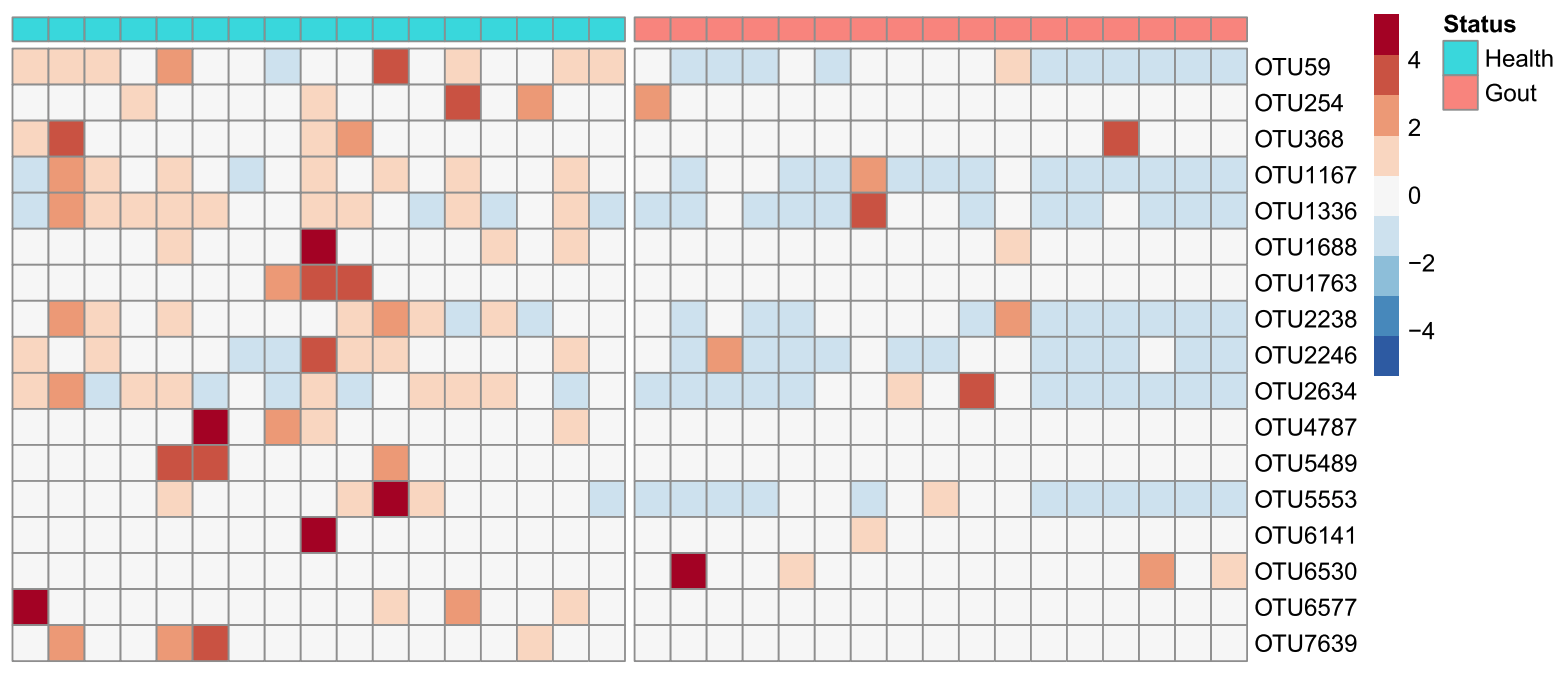   Two-sample test for compositional data with ball divergence

   Jin Zhu, Kunsheng Lv, Aijun Zhang, Wenliang Pan, and Xueqin Wang

   Statistics and Its Interface, Oct 2019

   Abs

   In this paper, we try to analyze whether the intestinal microbiota structures between gout patients and healthy individuals are different. The intestinal microbiota structures are usually measured by so-called compositional data, composed of multiple components whose value are typically non-negative and sum up to a constant. They are frequently collected and studied in many areas such as petrology, biology, and medicine nowadays. The difficulties to do statistical inference with compositional data arise from not only the constant restriction on the component sum, but also high dimensionality of the components with possible many zero measurements, which are frequently appeared in the 16S rRNA gene sequences. To overcome these difficulties, we first define the Bhattacharyya distance between two compositions such that the set of compositions is isometrically embedded in some spherical surfaces. And then we propose a two-sample test statistic for compositional data by Ball Divergence, a novel but powerful measure for the discrepancy between two probability measures in separable Banach spaces. Our test procedure demonstrates its excellent performance in Monte Carlo simulation studies even when the simulated data consist of thousand components with a high proportion of zero measurements. We also find that our method can distinguish two intestinal microbiota structures between gout patients and healthy individuals while the existing method does not.